Stanford: NLP with Machine Learning (1)

in AI on NLP


Lecture 1: Introduction and Word Vectors

Lecture Plan

Lecture 1: Introduction and Word Vectors

  1. The course (10 mins)
  2. Human language and word meaning (15 mins)
  3. Word2vec introduction (15 mins)
  4. Word2vec objective function gradients (25 mins)
  5. Optimization basics (5 mins)
  6. Looking at word vectors (10 mins or less)

How do we represent the meaning of a word?

1. As discrete symbols

  • “denotational semantics”: commonest linguistic way of thinking of meaning
  signifier (symbol) ⟺ signified (idea or thing)

aka. representational theory of meaning

  • How do we have usable meaning in a computer? Common solution: WordNet, a thesaurus containing Lists of synonym lists and hypernyms (“is a” relationships)
    • Problems
      • Great as a resource but missing nuance
      • Missing new meanings of words
      • subjective
      • Requires human labor to create and adapt
      • Can’t compute accurate word similarity

Representing words as discrete symbols

In traditional NLP, we regard words as discrete symbols: a localist representation: “hotel”, “conference”, “motel”, etc.

Words can be represented by one-hot vectors

  • motel = [ 0 0 1 0 ]
  • hotel = [ 0 1 0 0 ]

Problems The two vectors are orthogonal, no natural notion of similarity.

Solution:

  • Could try to reply on WordNet’s list of synonyms to get similarity?
    • But it is well-known to fail badly: incompleteness, etc.
  • Instead: learn to encode similarity in the vectors themselves

Representing words by their context

** Distributional semantics***: A word’s meaning is given by the words that frequently appear close-by

  • One of the most successful ideas of modern statistical NLP!

Word vectors

  • Build a dense vector for each word, chosen so that it is similar to vectors of words that appear in similar context.

  • word vectors are sometimes called word embeddings or word representations. They are distributed representations.

  • Word2vec (Mikolov et al. 2013) is a framework for learning word vectors
  • Idea
    • We have a large corpus of text
    • Every word in a fixed vocabulary is represented by a vector
    • Go through each position t in the text, which has a center word c and context (“outside”) words o
    • Use the similarity of the word vectors for c and o to calculate the probability of o given c (or vice versa)
    • Keep adjusting the word vectors to maximize this probability.
  • Objective function For each position \(t = 1, ..., T\), predict context words within a window of fixed size m, given a center word \(w_{j}\)
\[L (\theta) = \prod_{t = 1}^{T} \prod_{ -m \leq j \leq m \hspace{0.8mm} (j \neq 0) } P(w_{t+j}|w_{t};\theta)\]
  • \(\theta\) is all variables to be optimized

The objective function \(J(\theta)\) is the (average) negative log likelihood: \[J (\theta) = -\frac{1}{T}logL(\theta) = \prod_{t = 1}^{T} \prod_{ -m \leq j \leq m \hspace{0.8mm} (j \neq 0) } log P(w_{t+j}|w_{t};\theta)\]

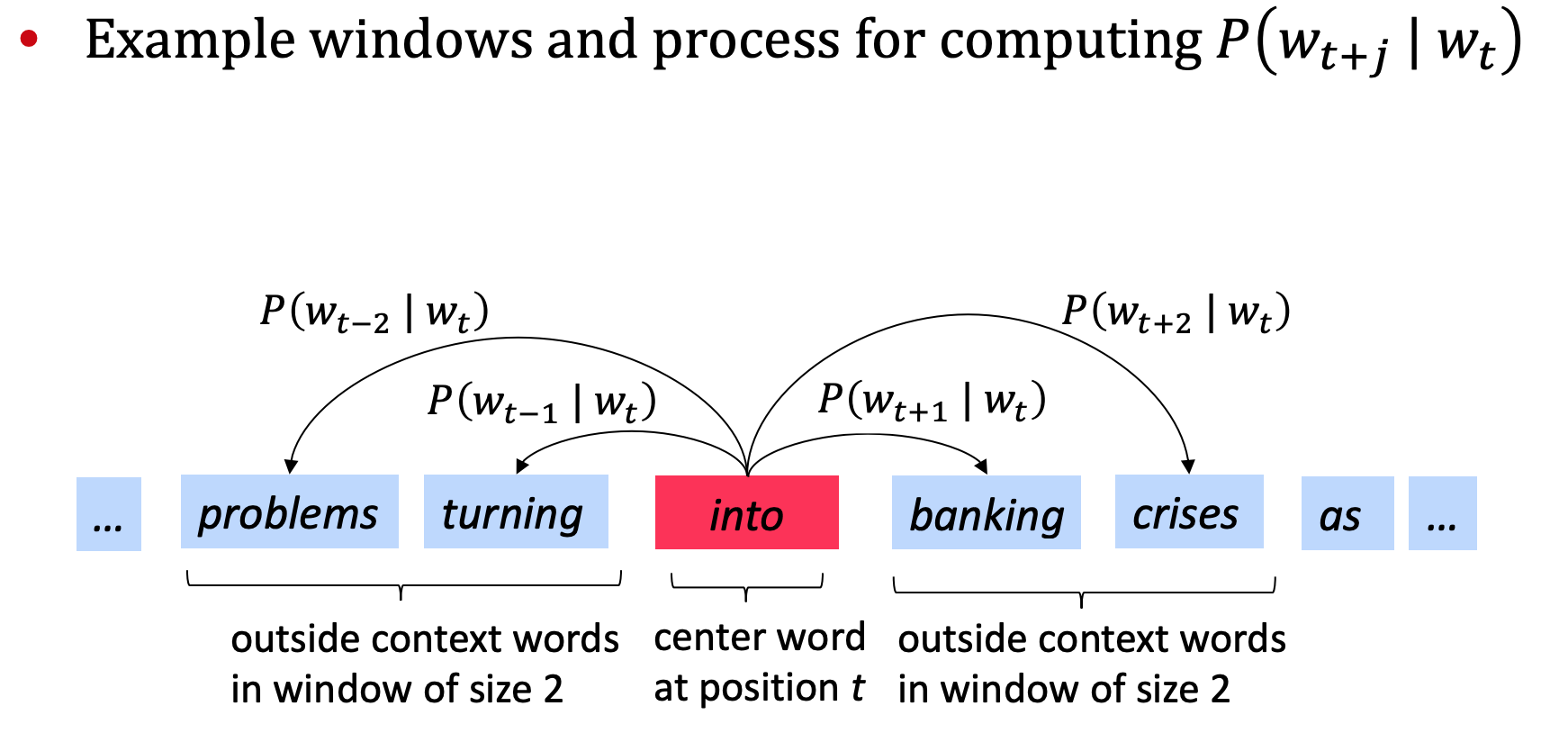
word2vec

  • Question: How to calculate \(P(w_{t+j} \| w_{t};\theta)\)?

    • Answer: We will use two vectors per word w:

      • \(v_{w}\) when w is a center word
      • \(u_{w}\) when w is a context word

Then for a center word c and a context word o: \[P(o|c) = \frac{exp(u_{o}^{T}v_{c})}{\sum_{w \in V} exp(u_{w}^{T}v_{c})}\]

  1. \(u_{o}^{T}v_{c}\): dot product compares similarity of o and c. \(u^{T}v = u v = \sum_{i=1}^n u_i v_i\) Larger dot product = larger probability

  2. Exponentiation makes anything positive \(exp(u_{o}^{T}v_{c})\)

  3. Normalize over entire vocabulary to give probability distribution \(\sum_{w \in V} exp(u_{w}^{T}v_{c})\) This is an example of the softmax function \(\mathbb{R}^n \rightarrow (0, 1)^n\)

\[softmax(x_i) = \frac{exp(x_i)}{\sum_{j=1}^n exp(x_j)} = p_i\]
  • The softmax function maps arbitrary values \(x_i\) to a probability distribution \(p_i\)
    • “max” because it amplifies probability of the largest \(x_i\)
    • “soft” because it still assigns some probability to smaller \(x_i\)
  • Train a model by optimizing parameters

To train a model, we adjust parameters to minimize a loss.

  • \(\theta\) represents all model parameters in one long vector
  • In our case with d-dimensional vectors and V-many words
\[\theta = \left[ \begin{array}{c} v_{aardvark} \\ v_a \\ \vdots \\ v_{zebra} \\ u_{aardvark} \\ u_a \\ \dots \\ u_{zebra} \end{array} \right] \in \mathbb{R}^{2dV}\]
  • Remember: every word has two vectors
  • We optimize these parameters by walking down the gradient

Two model variants

  1. Skip-grams (SG): Predict context (“outside”) words (position independent) given a center word
  2. Continuous Bag of Words (CBOW): Predict center word from (bag of) context words

The lecture assumed Skip gram model so far.

Reference







© 2020. by Changsin

Powered by changsin